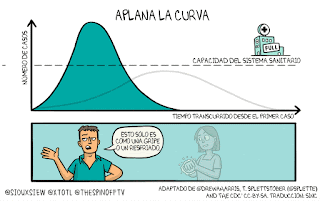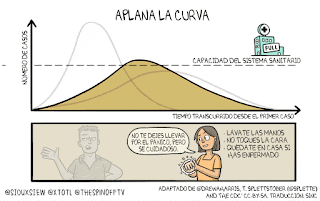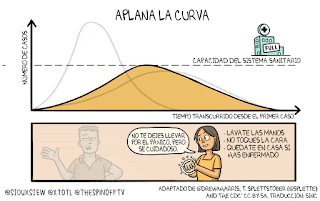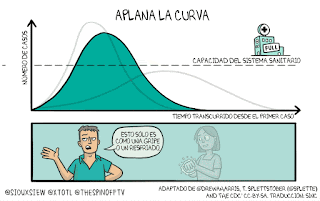
Desde ayer parece que por fin empezamos a llegar al "pico" de la famosa curva de contagios. Sabemos que tenemos que debemos quedarnos en casa para aplanar esa curva...
¿De verdad entendemos esto?
Dentro de las pocas cosas positivas que podría tener esta crisis, por fin mucha gente se ha dado cuenta de que las matemáticas sirven para algo más que operar o contar. Si profundizamos en el estudio de enfermedades encontraremos muchísimos conceptos de ESO y Bachillerato: fórmulas, progresiones, logaritmos, límites, derivadas,... y por supuesto funciones.
Llevamos muchos días deseando "aplanar" la curva, es decir, que la función pase de ser convexa a ser cóncava (aunque los matemáticos en funciones lo llamamos al revés). En términos técnicos (solo me entenderán los alumnos de 2º de Bachillerato y superiores), el objetivo de la primera fase ha sido que la función cambie el signo de la derivada segunda de positiva a negativa, pasando por un punto de inflexión, pues eso supone que el ritmo de contagios va disminuyendo hasta llegar al famoso pico (el máximo absoluto). En ese aplanamiento es donde intervenimos nosotros: si colaboramos y nos quedamos en casa, la velocidad de contagios disminuye y poco a poco tiende a cero (a partir del punto de inflexión, la pendiente de la recta tangente es cada vez menor hasta que la recta termina siendo horizontal).
¿Siguiente objetivo? Bajar del "pico". Eso será cuando la velocidad disminuya (función decreciente, con recta tangente de pendiente negativa), lo que nos obliga a seguir siendo responsables hasta el final.
Podéis ver la evolución de las curvas de cada país
en esta página. Si queréis más información, os recomiendo el artículo titulado "
Las matemáticas del coronavirus".